P1665 正方形计数题解
题目描述

思路
我们只要知道正方形一条对角线的两个点,那么一定能确定一个正方形。

比如上图,我们知道了 \(A\) 和 \(D\) 的位置并且将 \(A\) 和 \(D\) 作为对角线,那么一定能求出 \(B\) 和 \(C\) 的位置。
那我们来想一想怎么求。
- 首先连接正方形的两条对角线:

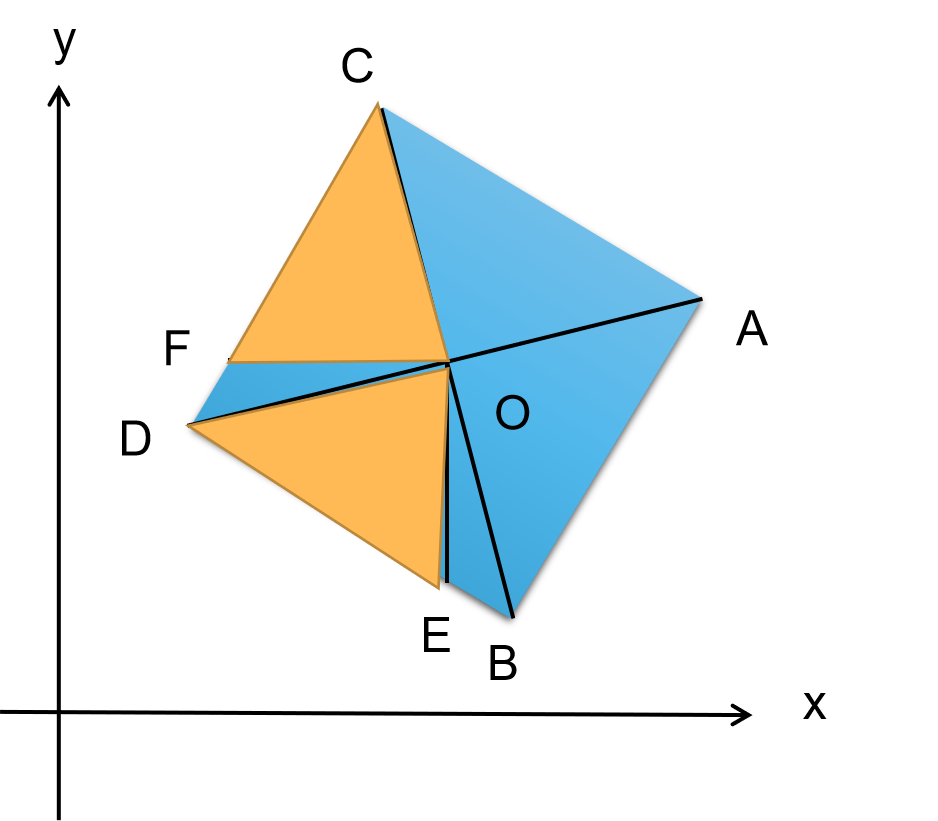
- 如图,我们从两条对角线的交点 \(O\) 作出与坐标轴平行的线段 \(OE, OF\):

-
然后我们可以用初二数学知识可知三角形 \(OFC\) 和 \(OED\) 全等(\(\text{SAS}\))。
同样我们利用初二数学知识可以求出 \(O\) 的坐标。
-
因为全等,我们可以得出它们的长度相等(\(dis1 = O_x - C_x = dis2\)):
注意:\(O\) 和 \(C\) 点坐标已知,所以 \(dis1\) 已知,可以求出 \(dis2\)。
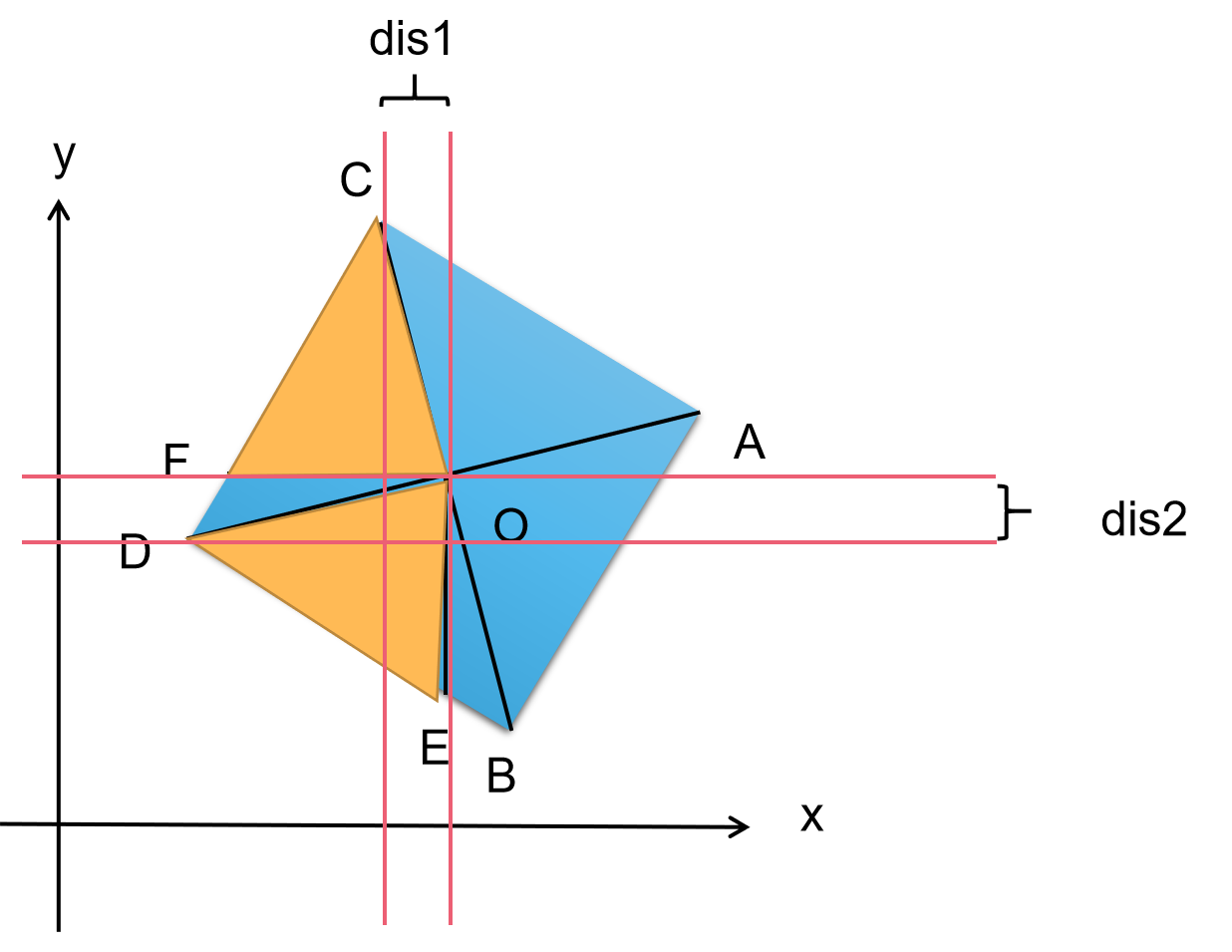
这样我们就可以利用了已知条件求出了 \(C\) 的横坐标 \(C_x = O_x - dis1 = O_x - dis2\)。
同样,我们可以得到 \(C\) 的纵坐标(下图) \(C_y = O_y + dis1 = O_y + dis2\)(\(dis1\) 已知,\(dis2\) 可以通过 \(dis1\) 求得)。
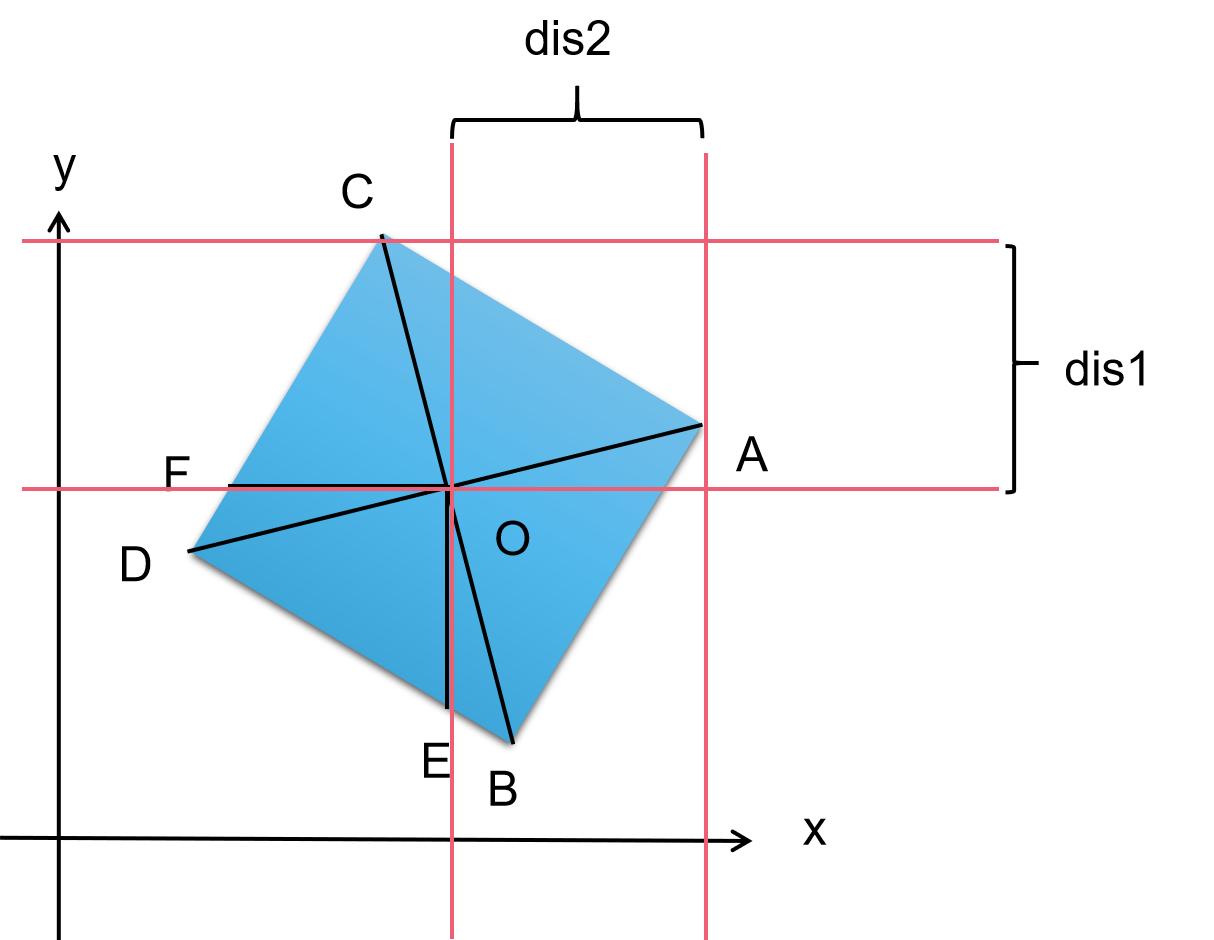
\(D\) 点的坐标求法类似。
代码
注意,我们为了不出现小数,所以我们将所有坐标乘以 \(2\)。
#include <bits/stdc++.h>
using namespace std;
using PII = pair<int, int>;
unordered_map<int, unordered_map<int, int>> m;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<PII> p(n);
for (auto& x : p) {
cin >> x.first >> x.second;
x.first *= 2;
x.second *= 2;
m[x.first][x.second] = 1;
}
int cnt = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int mx = (p[i].first + p[j].first) / 2, my = (p[i].second + p[j].second) / 2;
int x1 = mx - (my - p[i].second), x2 = mx + (my - p[i].second);
int y_1 = my + (mx - p[i].first), y2 = my - (mx - p[i].first);
if (m[x1][y_1] && m[x2][y2]) cnt++;
}
}
cout << cnt / 2 << '\n';
return 0;
}