2023.08.12 codeforces round 892 div2
年轻人的第三场div2(已完成:ABCDE)
rank:1265
solved:4
rating change:+276
new rating:1323
A.United We Stand
题意:给定一个数列a,问是否能分成两个非空的数列b和c,使得c中任意一个数不是b中任意一个数的因子;
若x是y的因子则有x<=y;因此不妨将数列的最大值放入c,把剩下的数放入b;注意数列中的数值全相同时无解;
1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 ll read(){ 5 char ch=getchar();ll x=0,f=1; 6 while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} 7 while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} 8 return x*f; 9 } 10 const int maxn=105; 11 ll T,N,lb,lc; 12 ll A[maxn]; 13 int main(){ 14 T=read(); 15 while(T--){ 16 N=read(); 17 int flag=false; 18 for(int i=1;i<=N;i++){ 19 A[i]=read(); 20 if(A[i]!=A[1])flag=true; 21 } 22 if(flag==false){ 23 cout<<"-1"<<endl; 24 } 25 else{ 26 sort(A+1,A+N+1); 27 int t=0; 28 for(int i=N;i>=1;i--){ 29 if(A[i]==A[N])t++; 30 } 31 cout<<N-t<<" "<<t<<endl; 32 for(int i=1;i<=N-t;i++){ 33 cout<<A[i]<<" "; 34 } 35 cout<<endl; 36 for(int i=N-t+1;i<=N;i++){ 37 cout<<A[i]<<" "; 38 } 39 cout<<endl; 40 } 41 } 42 return 0; 43 }
B.Olya and Game with Arrays
题意:给定N个数列,每个数列至少有两个数,可以将其中的最多一个数移动到别的数列(可以不移动),问每一列数的最小值的和的最大值是多少;
显然,所有数中最小的数一定要选;对于一个数列,由于我们最多只能移走一个数,因此,每一列数的最小值小于等于其次小值,每一列数最小值的和和 < 所有次小值的和;我们记录每一列数的最小值和次小值,我们不妨将所有的最小值移动的次小值最小的数列中去,即可令和=较大的N-1个次小值+所有数中最小的数;
1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 int read(){ 5 char ch=getchar();int x=0,f=1; 6 while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} 7 while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} 8 return x*f; 9 } 10 const int maxn=5e4+5; 11 const int maxm=1e9+7; 12 int T,N,M,tot; 13 int A[maxn],B[maxn][5]; 14 int main(){ 15 T=read(); 16 while(T--){ 17 N=read(); 18 tot=0; 19 ll ans=0,mi1=maxm,mi2=maxm,cnt1=0,cnt2=0; 20 for(int i=1;i<=N;i++){ 21 M=read(); 22 for(int j=1;j<=M;j++){ 23 A[j]=read(); 24 } 25 sort(A+1,A+M+1); 26 B[i][0]=A[1];B[i][1]=A[2]; 27 if(B[i][0]<mi1){ 28 mi1=B[i][0];cnt1=i; 29 } 30 if(B[i][1]<mi2){ 31 mi2=B[i][1];cnt2=i; 32 } 33 } 34 for(int i=1;i<=N;i++){ 35 if(i!=cnt2)ans+=B[i][1]; 36 if(i==cnt1)ans+=B[i][0]; 37 } 38 cout<<ans<<endl; 39 } 40 return 0; 41 }
C.Another Permutation Problems
题意:给定长度N,求对于N的所有排列对于该式子的最大值: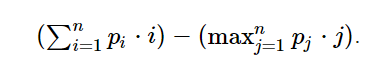
看了样例N=2和N=4的情况是将N和N-1换位置,其他数字按照原顺序,然后写了,然后样例后面几个数没过;于是推了一下5,发现5的最大值在排列为12543时取到,然后大胆猜想最大值是把最后的长度为x的区间翻转(比较对称(?))得到的,于是枚举长度x,写了,过了,但是没有证明;

1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 int read(){ 5 char ch=getchar();int x=0,f=1; 6 while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} 7 while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} 8 return x*f; 9 } 10 const int maxn=255; 11 int T,N; 12 int A[maxn]; 13 int main(){ 14 T=read(); 15 while(T--){ 16 N=read(); 17 ll ans=0; 18 for(int i=1;i<=N-1;i++)ans+=i*i; 19 for(int i=1;i<=N;i++){ 20 ll ma=0,sum1=0,sum2=0,t=0; 21 22 for(int j=1;j<i;j++)sum1+=j*j; 23 24 for(int j=i;j<=N;j++){ 25 t++; 26 sum2+=j*(N-t+1); 27 ma=max(ma,j*(N-t+1)); 28 } 29 ans=max(ans,sum1+sum2-ma); 30 } 31 cout<<ans<<endl; 32 } 33 return 0; 34 }
放一下正解(等有空了一定回来看()):

作者代码:
1 #include <iostream> 2 #include <algorithm> 3 #include <set> 4 #include <stack> 5 #include <vector> 6 using namespace std; 7 void solve() { 8 int N = 0; cin >> N; 9 int ans = 0; 10 vector<int> pr; 11 pr.assign(N * N, -1); 12 for (int i = 1; i <= N; ++i) { 13 for (int j = 1; j <= N; ++j) { 14 pr[i * j - 1] = 1; 15 } 16 } 17 for (int mx = N * N; mx >= 1; --mx) { 18 if (pr[mx - 1] == -1) continue; 19 vector<vector<int>> a; 20 int curans = -mx; 21 bool br = false; 22 a.assign(N, vector<int>()); 23 for (int j = N; j >= 1; --j) { 24 int num = min(mx / j, N); 25 if (num < 1) { 26 br = true; 27 break; 28 } 29 a[num - 1].push_back(j); 30 } 31 if (br) break; 32 stack<int> s; 33 for (int i = 0; i < N; ++i) { 34 s.push(i + 1); 35 bool brk = false; 36 for (auto x : a[i]) { 37 if (s.empty()) { 38 brk = true; break; 39 } 40 curans += s.top() * x; 41 s.pop(); 42 } 43 if (brk) break; 44 } 45 ans = max(ans, curans); 46 } 47 cout << ans << "\n"; 48 } 49 50 int main() { 51 ios_base::sync_with_stdio(false); 52 cin.tie(nullptr); 53 int t = 0; cin >> t; 54 while (t--) solve(); 55 return 0; 56 }
D.Andrey and Escape from Capygrad
题意:跑路,有很多传送门,对于给定的一个传送门,有四个相关的参数l,r,a,b,有l<=a<=b<=r;如果一个人的位置x有l<=x<=r,那么传送门可以把他传送到任意y(a<=y<=b)现在给定Q个询问,每个询问给定一个人初始位置,问能到达的最远位置;
显然对于给定的四个参数l,r,a,b,只有l,b是对答案有影响的,其实原式等价于当一个人的位置为x(l<=x<=b)时最远可以到达b,因为如果位置大于b时最远只能在原位;
对于给定的传送门,我们先进行排序操作,然后对于有重叠部分的我们直接合并成一个新的传送门,对于询问的起始点x二分查找(佬用的upper_bound)第一个l<=x的传送门,并比较x和该传送门能到达的最远位置;
题解用的离线查询+扫描线;
1 #include<bits/stdc++.h> 2 using namespace std; 3 int read(){ 4 char ch=getchar();int x=0,f=1; 5 while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} 6 while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} 7 return x*f; 8 } 9 const int maxn=2e5+5; 10 int T,N,Q,tot; 11 struct node{ 12 int l,r,a,b; 13 }e[maxn]; 14 struct no{ 15 int l,r; 16 }t[maxn]; 17 int cmp(node x,node y){ 18 if(x.l==y.l)return x.b<y.b; 19 return x.l<y.l; 20 } 21 int check(int mid,int x){ 22 if(x>=t[mid].l)return 1; 23 return 0; 24 } 25 int main(){ 26 T=read(); 27 while(T--){ 28 N=read(); 29 for(int i=1;i<=N;i++){ 30 e[i].l=read();e[i].r=read();e[i].a=read();e[i].b=read(); 31 } 32 sort(e+1,e+N+1,cmp); 33 tot=1;t[tot].l=e[1].l,t[tot].r=e[1].b; 34 for(int i=1;i<=N;i++){ 35 if(e[i].l<=t[tot].r){ 36 t[tot].r=max(t[tot].r,e[i].b); 37 continue; 38 } 39 else{ 40 tot++;t[tot].l=e[i].l;t[tot].r=e[i].b; 41 } 42 } 43 Q=read(); 44 for(int i=1;i<=Q;i++){ 45 int x=read(); 46 int L=1,R=tot,ans=0; 47 while(L<=R){ 48 int mid=(L+R)>>1; 49 if(check(mid,x))ans=mid,L=mid+1; 50 else R=mid-1; 51 } 52 cout<<max(t[ans].r,x)<<" "; 53 } 54 cout<<endl; 55 for(int i=1;i<=N;i++){ 56 e[i].l=e[i].r=e[i].a=e[i].b=0; 57 t[i].l=t[i].r=0; 58 } 59 } 60 return 0; 61 }
E.Maximum Mogonosity
题意:给定两个长度为 N 的数列 A 和 B,定义区间 [ l , r ] 的 cost 为 f ( l , r ) = abs ( Al - Br ) + abs ( Ar - Bl ) ;求总长度为 K 的不相交的区间的 cost 的和的最大值;
定义 dp [ n1 ] [ k1 ] 为区间总长度为k1,所有不相交的区间都有 r < n1 的 cost 的和的最大值;
可以得到状态转移方程:dp [ n1 ] [ k1 ] = max ( dp [ n1-1 ] [ k1 ] , dp [ n1-l ] [ k-l ] + f ( n1-l+1 , n1 ) );
由绝对值的性质可以得到 abs ( a - b ) + abs ( c - d ) = max ( a - b + c - d , a - b - c + d , - a + b + c - d , - a + b - c + d ) ;
优化:用 mx 数组维护前面的区间的最大值,详情见代码注释:
1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 ll read(){ 5 char ch=getchar();ll x=0,f=1; 6 while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();} 7 while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} 8 return x*f; 9 } 10 const int maxn=3e3+5; 11 ll T,N,K; 12 ll A[maxn],B[maxn],dp[maxn][maxn],f[maxn][maxn]; 13 ll mx1[maxn],mx2[maxn],mx3[maxn],mx4[maxn]; 14 int main(){ 15 T=read(); 16 while(T--){ 17 N=read();K=read(); 18 for(int i=1;i<=N;i++)A[i]=read(); 19 for(int i=1;i<=N;i++)B[i]=read(); 20 21 for(int i=0;i<=N;i++){ 22 mx1[i]=B[i+1]-A[i+1]; 23 mx2[i]=B[i+1]+A[i+1]; 24 mx3[i]=-B[i+1]-A[i+1]; 25 mx4[i]=-B[i+1]+A[i+1]; 26 }//以i+1作为下一个区间的l 27 //mx数组表示:当前的dp值+下一个区间的fl的最大值; 28 29 //dp[n1][k1]=max(dp[n1-1][k1],dp[n1-l][k1-l]+fl(n1-l+1)+fr(n1));fl(x)与fr(x)分别表示以x作为区间的l和r时的值; 30 //mx[n1-k1]=max(dp[n1-l][k1-l]+fl(n1-l+1)); 31 32 for(ll i=1;i<=N;i++){//n1; 33 for(ll j=1;j<=min(i,K);j++){//k1; 34 dp[i][j]=dp[i-1][j]; 35 dp[i][j]=max(dp[i][j],mx1[i-j]+B[i]-A[i]); 36 dp[i][j]=max(dp[i][j],mx2[i-j]-B[i]-A[i]); 37 dp[i][j]=max(dp[i][j],mx3[i-j]+B[i]+A[i]); 38 dp[i][j]=max(dp[i][j],mx4[i-j]-B[i]+A[i]); 39 //dp值取四种情况的最大值; 40 //max(dp[n1-1][k1],mx[n1-k1]+fr[n1]); 41 if(i<N){ 42 mx1[i-j]=max(mx1[i-j],dp[i][j]+B[i+1]-A[i+1]); 43 mx2[i-j]=max(mx2[i-j],dp[i][j]+B[i+1]+A[i+1]); 44 mx3[i-j]=max(mx3[i-j],dp[i][j]-B[i+1]-A[i+1]); 45 mx4[i-j]=max(mx4[i-j],dp[i][j]-B[i+1]+A[i+1]); 46 }//维护dp的两个维度的差值一定时的最大值; 47 } 48 } 49 cout<<dp[N][K]<<endl; 50 } 51 return 0; 52 }