侦察守卫

yonglicp / 2023-08-12 / 原文

传送门：https://www.luogu.com.cn/problem/P3267

给与n,d。给与n的整数表示每个节点放侦察兵的价钱。每个侦察兵可以看到d远。

给与m, 接下来有m个节点表示有人。

接下来给与n-1行表示树的边。

求看到所有人的最佳价钱。(n<=5e5, d<=20)

解：复杂度 O(nd)

我们设计两个数组 f 和 g ：

令f [ i ][ j ] 为当我们还没看到以 i 为子树的接下来 j 深，但是以下的都已经涂了 + 往上涂 j 高的最价钱

令g [ i ][ j ] 为当我们还没看到以 i 为子树已经涂满 + 往上涂 j 高的最价钱

有点复杂那么画个图吧：

如果现在考虑u和v, u为v的父亲

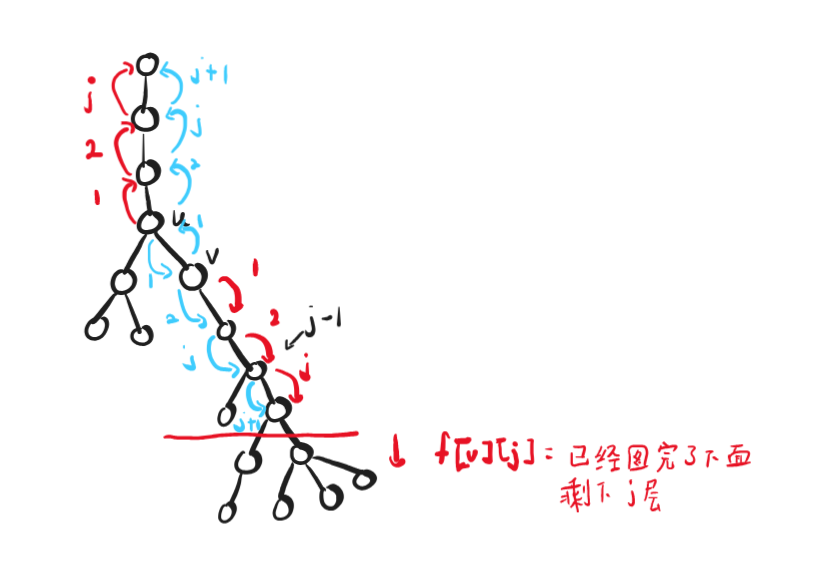
初始化的状态为:

若u有人: f[u][0]=g[u][0]=cost[u]

g[u][j]=cost[u] j->[1,d]

g[u][d+1]=inf

而答案显而易见就是 g[1][0]

转移状态有点复杂：

那么 g[u][j] = min( g[u][j]+ f[v][j], g[v][j+1] + f[u][j+1] );

f[u][0]=g[u][0]应该蛮明显的嘛, 毕竟往上走0步就是一样的

而 f[u][j] += f [v][j-1]

不过我们这里就需要对g[u][]取后缀最小值，f[u][]取前缀最小值

代码如下：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf = 1e16, N = 5e5 + 500;
int g[N][22], f[N][22];
signed main() {
	ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int n, d; cin >> n >> d;
	vector<vector<int>> adj(n + 1);
	vector<int> c(n + 1), V(n + 1);
	for (int i = 1; i <= n; i++) cin >> c[i];
	int m; cin >> m; for (int i = 1; i <= m; i++) { int x; cin >> x; V[x] = 1; }
	for (int i = 0; i < n - 1; i++) {
		int u, v; cin >> u >> v;
		adj[u].push_back(v);
		adj[v].push_back(u);
	}
	function<void(int, int)> dfs = [&](int u, int fa) {
		if (V[u]) g[u][0] = f[u][0] = c[u];
		for (int i = 1; i <= d; i++) g[u][i] = c[u];
		g[u][d + 1] = inf;
		for (auto& v : adj[u]) {
			if (v == fa) continue;
			dfs(v, u);
			for (int i = d; i >= 0; i--) g[u][i] = min(g[u][i] + f[v][i], g[v][i + 1] + f[u][i + 1]);
			for (int i = d; i >= 0; i--) g[u][i] = min(g[u][i], g[u][i + 1]);
			f[u][0] = g[u][0];
			for (int i = 1; i <= d + 1; i++) f[u][i] += f[v][i - 1];
			for (int i = 1; i <= d + 1; i++) f[u][i] = min(f[u][i], f[u][i - 1]);
		}
	};
	dfs(1, 0);
	cout << g[1][0] << '\n';
}
//nyl,加油!