tzoj1471 wall（凸包模板题）

yosuganosora / 2023-08-12 / 原文

题目大意

　　　　　　n个点构成的城堡，给出每个点的坐标。若要修建距离城堡最近距离为L的城墙，问城墙的最短长度。

　　　　　　凸包模板题，用Andrew算法求出凸包然后加上半径为L的圆的周长即可。

　　　　　　题目链接

Andrew算法

　　　　　　首先对所有点按照x大小进行升序排序，如果x相同就按照y大小升序排序。

构造下凸包　　

　　　　　　前两个点直接入栈。随后遍历其他点，利用叉积判断每个点能否于它的前两个点构成凸多边形。

　　　　　　如果是就入栈。

　　　　　　如果不是就回溯，不断地删除最后一个入栈的点，直到栈中只剩下一个点或者栈顶的两个点能与当前的点构成凸多边形。

构造上凸包

　　　　　　与构造下凸包同理。回溯时要注意不能删除下凸包的点。

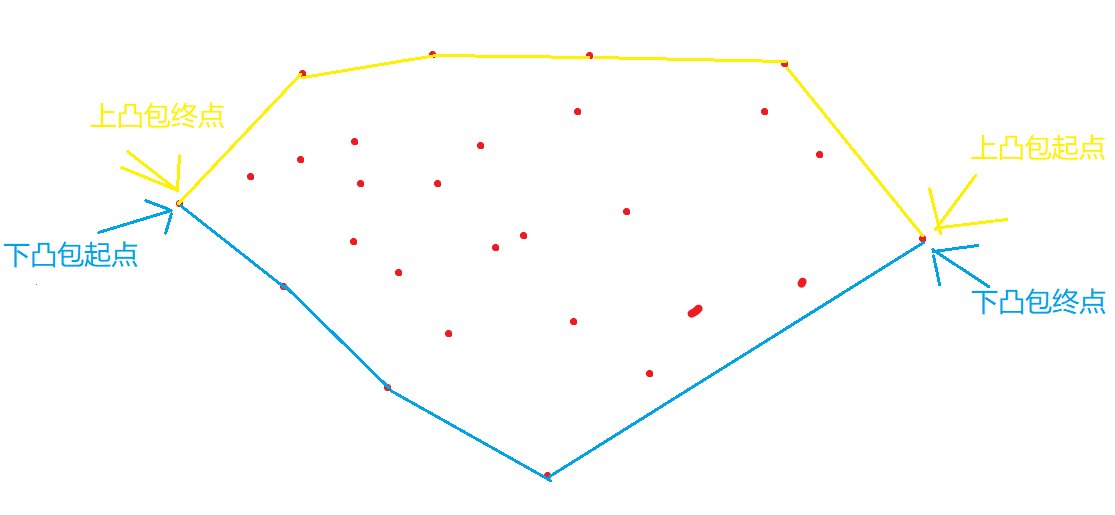
可以看到上下凸包是相连的。最终答案就是这两个合并起来。

代码

#include <bits/stdc++.h>
#define IO ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
using namespace std;

const int N = 1001;
int n, tot;
struct node
{
    double x, y;
} a[N], p[N];

double dis(node A,node B)
{
    return sqrt((B.x - A.x) * (B.x - A.x) + (B.y - A.y) * (B.y - A.y));
}
 
double cross(node A,node B,node C)
{
    return (B.x - A.x) * (C.y - A.y) - (C.x - A.x) * (B.y - A.y);
}
bool cmp(node A,node B)
{
    if(A.x!=B.x)
        return A.x < B.x;
    return A.y < B.y;
}
void Andrew(double l)
{
    sort(a + 1, a + n + 1, cmp);
    tot = 0;
    for (int i = 1; i <= n; i++)
    {
        while(tot>1&&cross(p[tot-1],p[tot],a[i])<=0)
            tot--;
        p[++tot] = a[i];
    }
    double ans = 0;
    int temp = tot;
    for (int i = n - 1; i >= 1; i--)
    {
        while(tot>temp&&cross(p[tot-1],p[tot],a[i])<=0)
            tot--;
        p[++tot] = a[i];
    }
    for (int i = 1; i < tot;i++)
    {
        ans += dis(p[i], p[i + 1]);
    }
    cout << int(ans + 2.0 * acos(-1) * l + 0.5) << endl;
}
signed main()
{
    IO;
    double l;
    cin >> n >> l;
    for (int i = 1; i <= n;i++)
        cin >> a[i].x >> a[i].y;
    Andrew(l);
    return 0;
}