【图论】最小生成树
什么是最小生成树
给定一个图,在图中选择N - 1条边(N代表图的点数)把图的所有节点都连起来,且边的权值最小,则这N - 1条边就是原图的最小生成树。
如何求最小生成树
求最小生成树有两种算法:
-
prim
-
kruskal
prim算法
其实本质上和dijstra算法很像。
适用于稠密图。
题目:
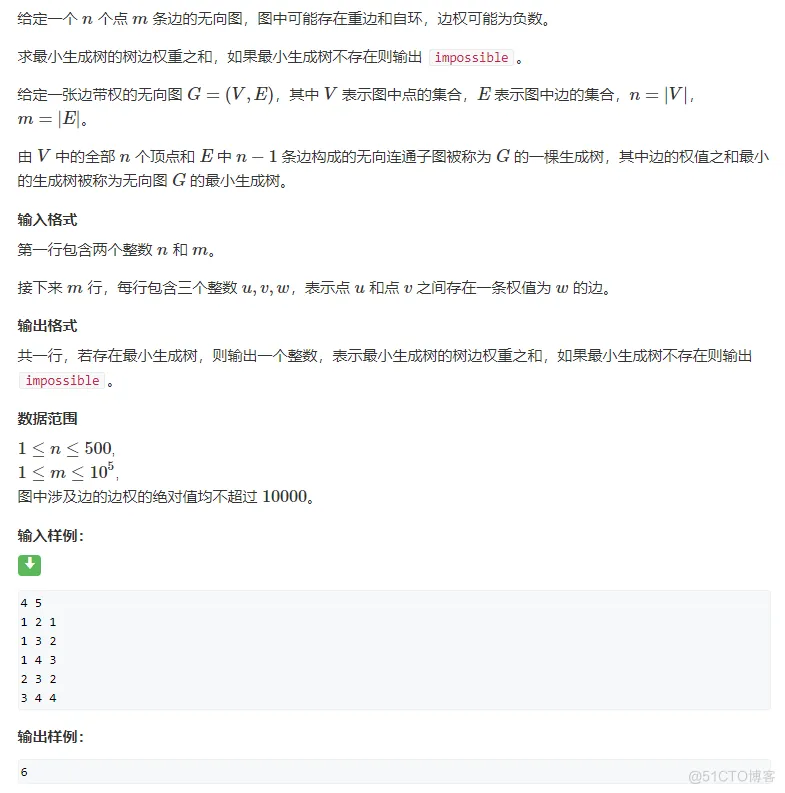
算法流程:
-
将所有点到已经选的点的集合的距离设为正无穷。
-
每次找到dis最小的点,加入到集合中。
-
使用该点的距离更新所有点到集合距离(注意:我们之前已经确定过的点不需要再被改变dis,所以说我们要特殊确定一下)。
代码:
#include <bits/stdc++.h>
#define N 510
using namespace std;
int n, m;
int g[N][N];
int dis[N];
bool st[N];
int prim() {
memset(dis, 0x3f, sizeof dis);
dis[1] = 0;
int ans = 0;
for (int i = 1; i <= n; ++i) {
int minid = -1; // dis最小的点
for (int j = 1; j <= n; ++j)
if (!st[j] && (minid == -1 || dis[j] < dis[minid]))
minid = j;
if (dis[minid] == 0x3f3f3f3f)
return 0x3f3f3f3f; // 不符合条件
ans += dis[minid];
st[minid] = true;
for (int j = 1; j <= n; ++j)
dis[j] = min(dis[j], g[minid][j]); // 更新距离
}
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
memset(g, 0x3f, sizeof g);
cin >> n >> m;
while (m--) {
int a, b, c;
cin >> a >> b >> c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int t = prim();
if (t == 0x3f3f3f3f)
puts("impossible");
else
cout << t << '\n';
return 0;
}
kruskal算法
适用于稀疏图。
题目:
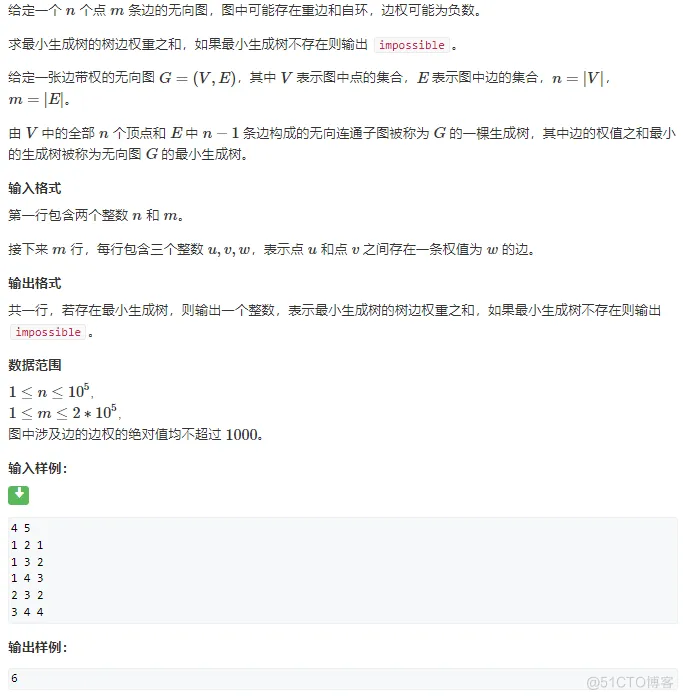
前置知识:并查集
如果不会并查集,可以看我的另外一篇博客:【数据结构】并查集
算法流程:
- 将所有边按照权值从小到大排序。
- 如果这条边与之前选出来的所有边不会形成环(使用并查集判断),那么就使用这条边,否则舍去这条边。
- 直到选出了N-1条边,算法结束。
代码:
#include <bits/stdc++.h>
#define N 100010
using namespace std;
int p[N]; // 并查集
struct Egde {
int a, b, c;
bool operator<(const Egde& t) const {
return c < t.c;
} // 按边权从小到大排序
} edges[N * 2];
int n, m;
int cnt, ans;
int find(int x) {
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
void kruskal() {
for (int i = 1; i <= m; ++i) {
int a = find(edges[i].a), b = find(edges[i].b), c = edges[i].c;
if (a != b) {
ans += c;
cnt++;
p[a] = b;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i)
p[i] = i;
for (int i = 1; i <= m; ++i) {
int a, b, c;
cin >> a >> b >> c;
edges[i] = {a, b, c};
}
sort(edges + 1, edges + m + 1);
kruskal();
if (cnt < n - 1) { // 选出的边数不是N-1条,不符合条件
puts("impossible");
return 0;
}
cout << ans << '\n';
return 0;
}