Tarjan缩点

zhujio / 2023-08-06 / 原文

P3225 [HNOI2012] 矿场搭建

一共只会删除一个点，将每个点双连通分量分三种情况讨论

第一种：点双连通分量没有割点，那么为了保证一定可以逃出去，至少需要两个点

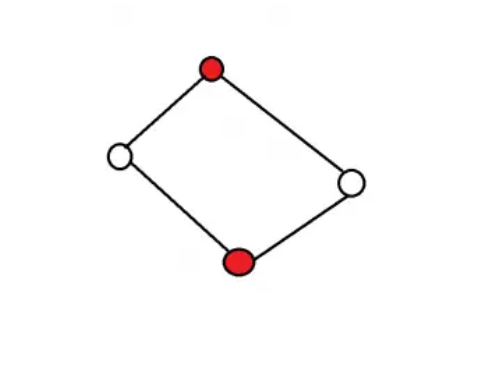
第二种：点双连通分量有且只有一个割点，此处割点是绿色的点，那么对于这种点双连通分量

就需要在每个只有一个割点的双连通分量中设置一个逃生点

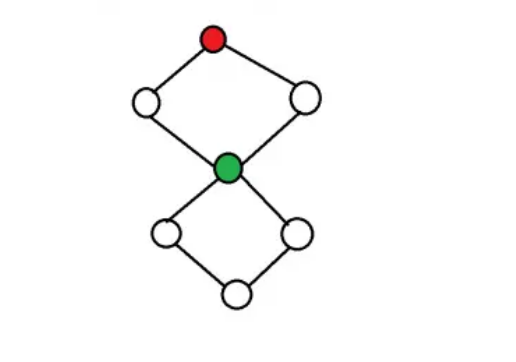
第三种：点双连通分量有割点并且大于一个，此处对于双连通分量 { 1，2，3 } 中有割点2 1，那么对于这种点双连通分量不需要做任何处理

因为只会塌方一个点，并且由第二种情况，每个只有一个割点的双连通分量都会设置一个逃生点，那么第三种双连通分量某个割点塌方的话

他依旧可以从另外的割点逃出去，一直逃到逃到只有一个割点的双连通分量

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"
#define int long long
typedef long long ll;


const int N=505;

std::vector<int>edge[N],cc[N];

int dfn[N],low[N],cut[N],idx,m,cnt;
stack<int>stk;

void dfs(int x,int fa,int root){
    dfn[x]=low[x]=++idx;
    stk.push(x);
    int son=0;
    //判断孤立点
    if(x==root&&(int)edge[x].size()==0){
        cut[x]=1;
        ++cnt;
        cc[cnt].push_back(x);
        return;
    }
    for(auto y:edge[x]){
        if(!dfn[y]){
            dfs(y,x,root);
            son++;
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]){
                cut[x]=1;
                ++cnt;
                cc[cnt].push_back(x);
                while(1){
                    int top=stk.top();
                    cc[cnt].push_back(top);
                    stk.pop();
                    if(top==y)break;
                }
            }
        }else if(y!=fa){
            low[x]=min(low[x],dfn[y]);
        }
    }  
    if(x==1&&son<=1)cut[x]=0;
}

int main(){
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int cs=0;
    while(1){
        ++cs;
        int m;cin>>m;
        if(!m)break;
        int n=0;
        for(int i=1;i<=m;i++){
            int x,y;cin>>x>>y;
            edge[x].push_back(y);
            edge[y].push_back(x);
            n=max({n,x,y});
        }
        for(int i=1;i<=n;i++){
            low[i]=dfn[i]=cut[i]=0;
        }
        while(!stk.empty())stk.pop();
        idx=cnt=0;
        for(int i=1;i<=n;i++){
            if(!dfn[i])dfs(i,i,i);
        }
        cout<<"Case "<<cs<<": ";
        int ans1=0,ans2=1;
        for(int i=1;i<=cnt;i++){
            int ncut=0;
            for(auto j:cc[i])ncut+=cut[j];
            if(ncut==0){
                ans1+=2;
                ans2*=(int)cc[i].size()*((int)cc[i].size()-1)/2;
            }else if(ncut==1){
                ans1+=1;
                ans2*=(int)cc[i].size()-1;
            }
        }
        cout<<ans1<<' '<<ans2<<endl;
        for(int i=1;i<=n;i++)edge[i].clear(),cc[i].clear();
    }
    return 0;
}