网络流入门
网络流是什么?
网络流是 OI 图论中的内容,比较有用的是网络最大流与费用流。
网络流就像一个复杂的水网,它有一个源点 \(S\),可以供应无穷无尽的水,有一个汇点 \(T\),要让水从源点流到汇点,我们就连上了许多水管,也就是边,中间有一些中转站连接不同的水管,也就是点,每条水管都有一个流量上限,叫做容量,如果超过了容量就会炸裂,所以我们不能灌入比该水管流量上限更多的水,空闲量就是该边还可以通过的水的容量。
比如下图,图中的边就相当于水管,边上的数字(权值)就是每条边的流量上限。
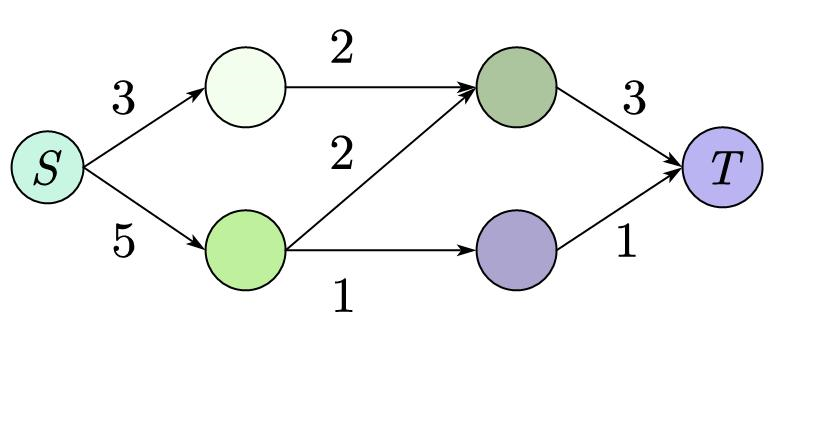
这是将水输送到 \(T\) 一种合法的方案:
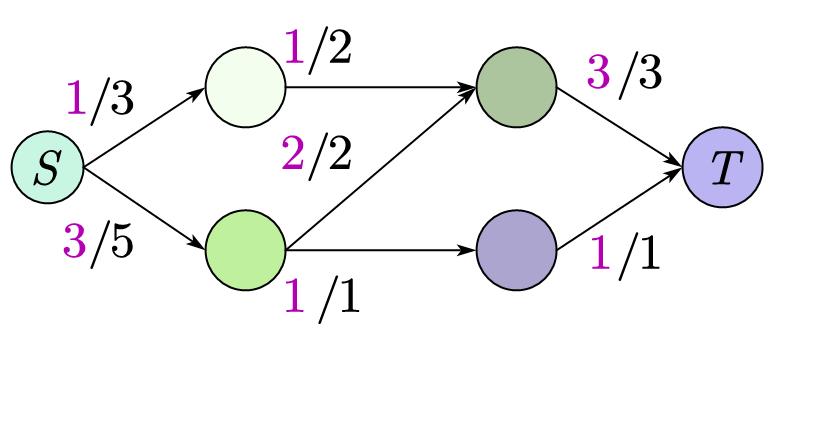
其中紫色数字是水流大小 \(d\),黑色数字是容量 \(f\),其中,一定有 \(d \leq f\):
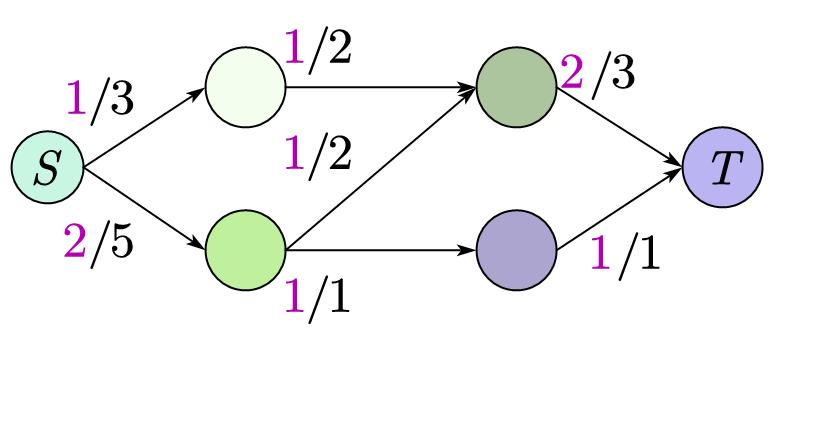
那这个图的的流量就是 \(3\),我们既可以看源点也可以看汇点得出(\(1 + 2 = 3\))。
找阻塞流
如果我们不能从源点输送更多的水到汇点,那么这个水流的状态就叫阻塞流。
上图就不是一个阻塞流,因为实际上可以从源点往容量为 \(3\) 的水管再输送 \(1\) 的水。
我们还要知道:
空闲量 = 容量 - 流量
即空闲量表示还可容纳多少水。
首先,我们建出以空闲量为权值的图 \(G\),最开始时没有水流通过,所以该图等于原图。

然后我们随便从图 \(G\) 中找出从 \(S\) 和 \(T\) 的简单路径,我们现在就要让这条路径尽它的最大能力输送水,
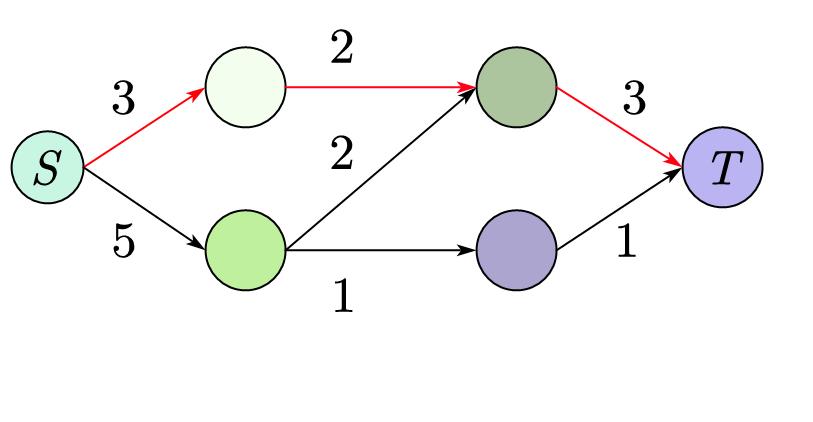
取到这条路径上最小的权值 \(w\),再将所有的权值减去 \(w\),表示有 \(w\) 的水流过,空闲量减少了 \(w\)。
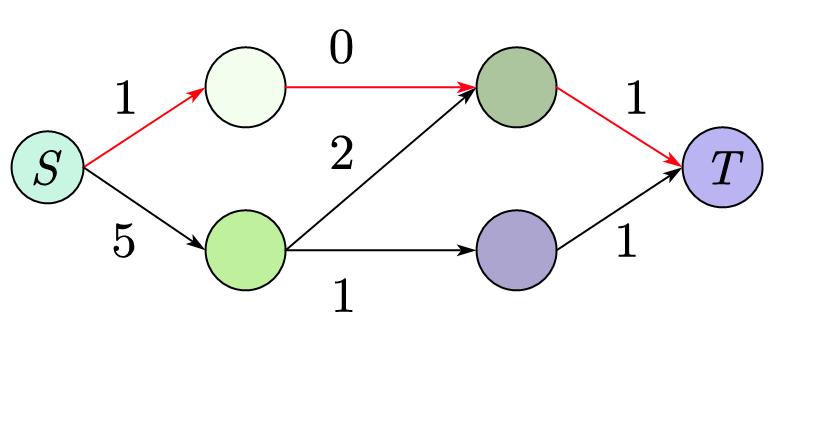
然后再将所没用的边去掉,即容量为 \(0\) 的边。
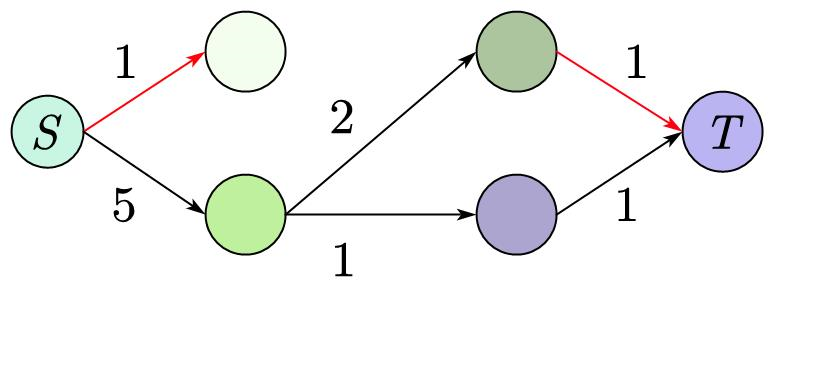
不断重复上述步骤,
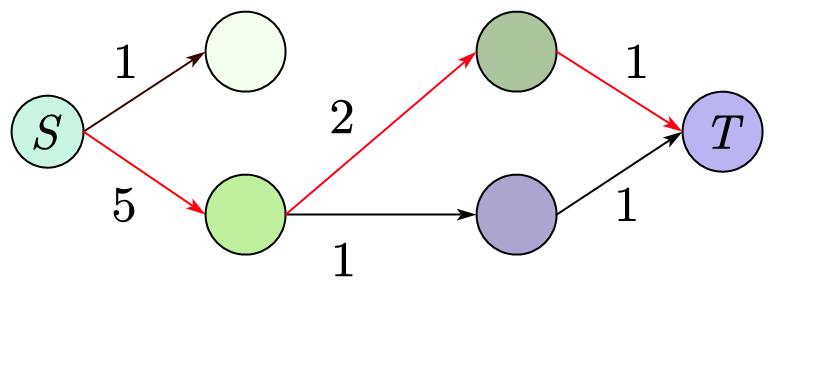
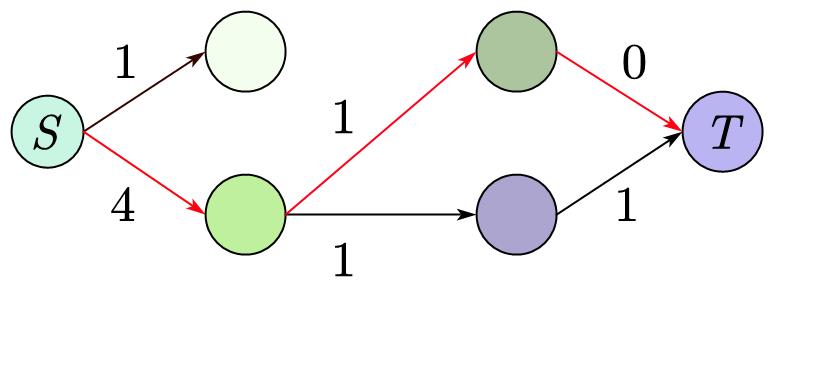
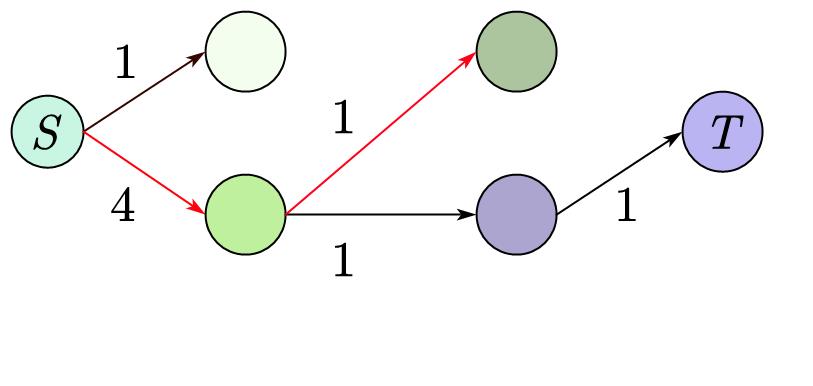
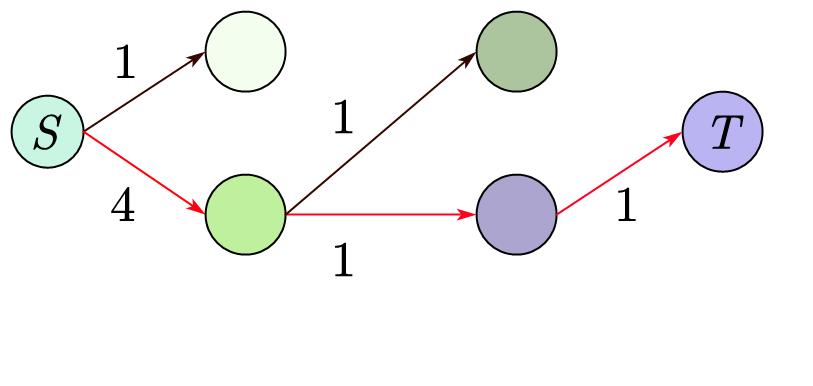
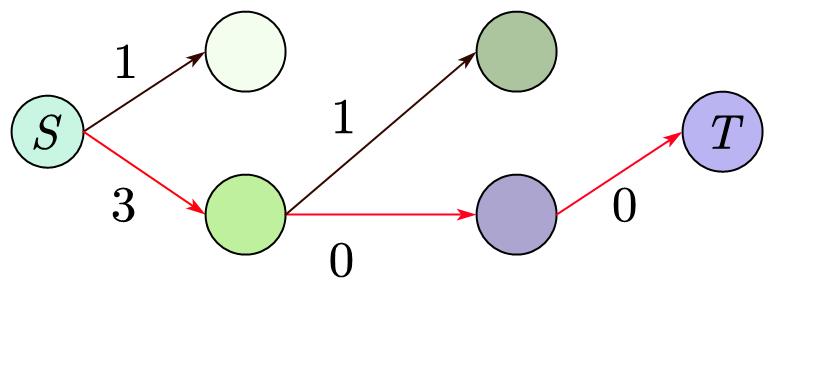
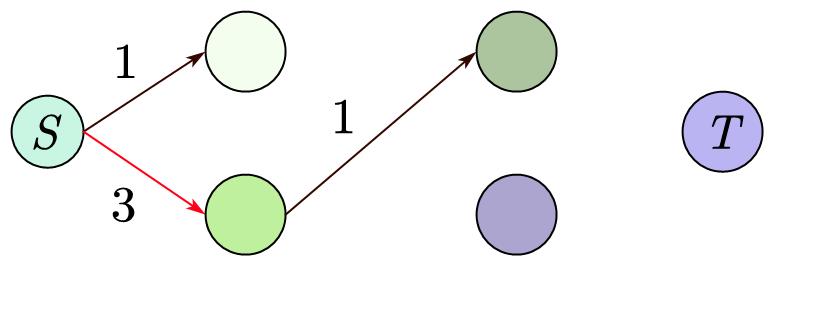
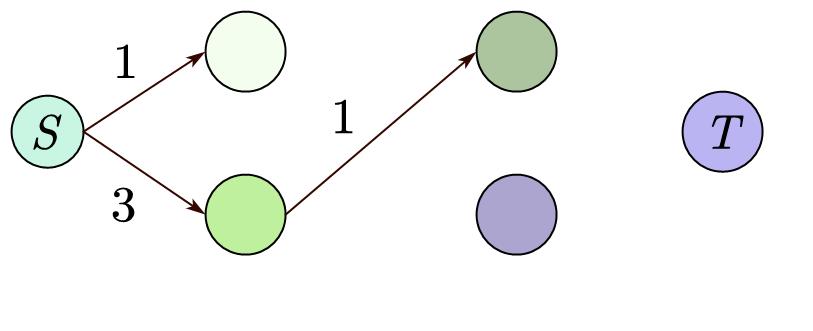
当我们已经找不到路径了,我们就可以停止了。
我们把刚刚减去 \(w\) 全部累加起来,就得到了阻塞流。
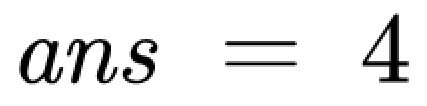
网络最大流
什么是网络最大流呢?
就是在不超过容量的情况下,从源点输送更多的水到汇点。
比如上图的网络最大流就是 \(4\),不可能再输送更多的水从 \(S\) 到 \(T\):
那么我们怎么求网络最大流呢?
有很多算法可以办到,比如 Ford–Fulkerson,EK,dinic 算法。
可以这么理解 EK 是 Ford–Fulkerson 的优化,dinic 是 EK 的优化。
Ford–Fulkerson 算法
首先,我们发现再刚刚找阻塞流的时候就是一个劲地往下找,
运气不好就找不到网络最大流,比如下面这个例子(注意不是上面那个图),
找到的阻塞流为 \(3\),最大流其实是 \(4\):
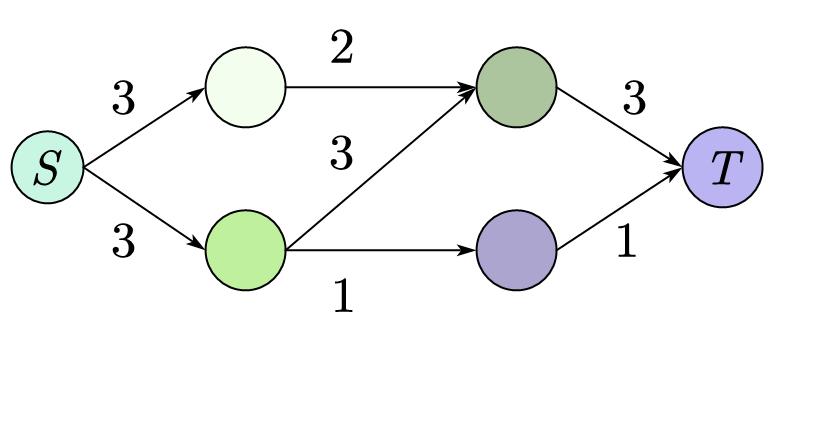
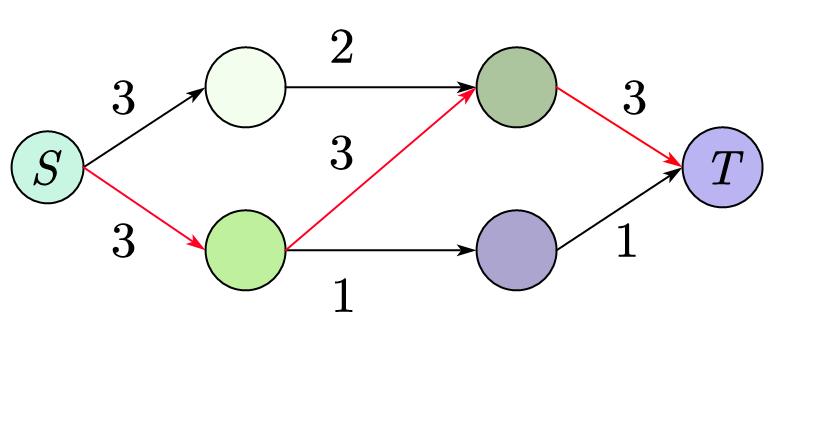
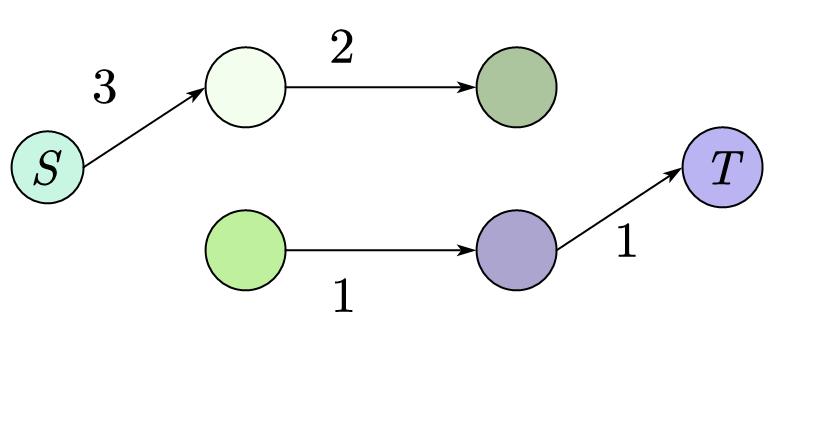
其实,我们可以建立一条反向边。
让水倒着流回去,比如:
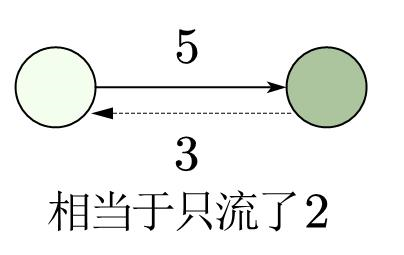
那么我们在找阻塞流的时候顺便加上一条容量相同的反向边就实现了“可以后悔”的做法,
即找错了边也不要紧,再回来不就完了。
算法过程就变成了:
- 随便找一条从 \(S\) 到 \(T\) 的路径,与找阻塞流一样;
- 然后取该边上最小的权值 \(w\),让所有的边都减去 \(w\),与找阻塞流一样;
- 建立一条权值为 \(w\) 的反边,可以让水流原路流回去。
比如下图,图中虚线是反边,红色边是找到的路径(正反边皆可),紫色数字是反边权值,黑色数字是原边权值:
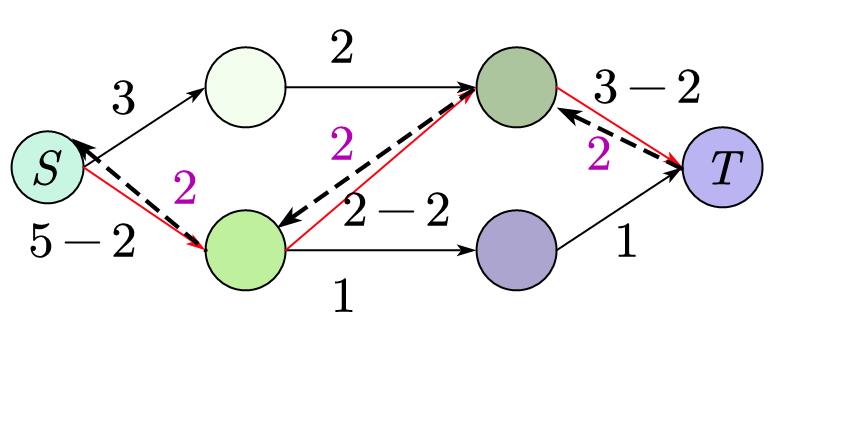
然后不断重复以上步骤,直到找不到路径为止。
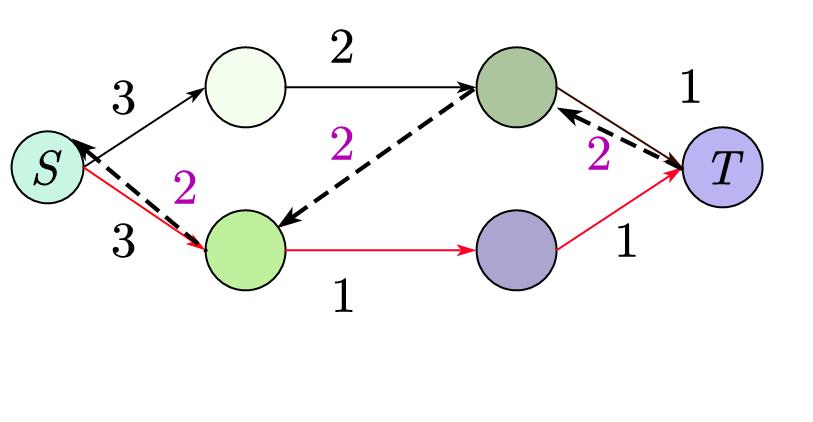
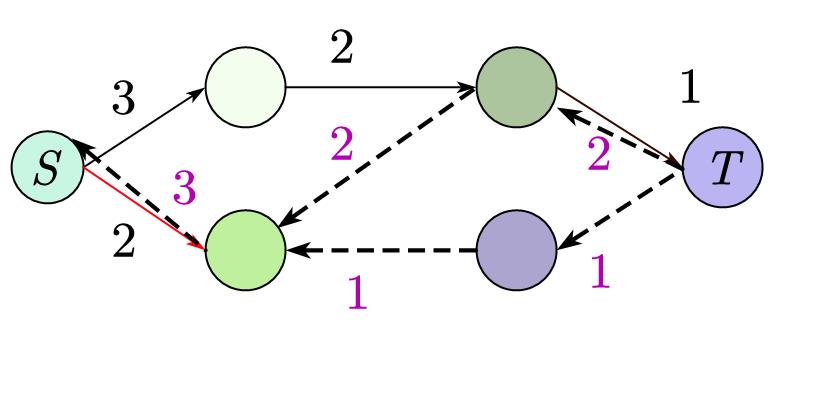
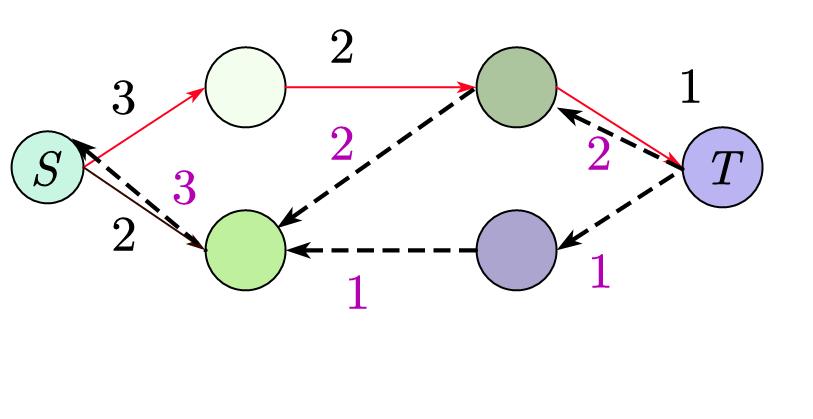
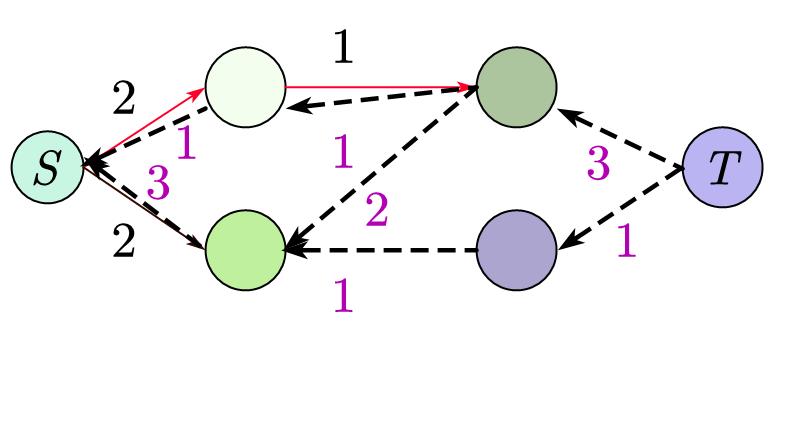
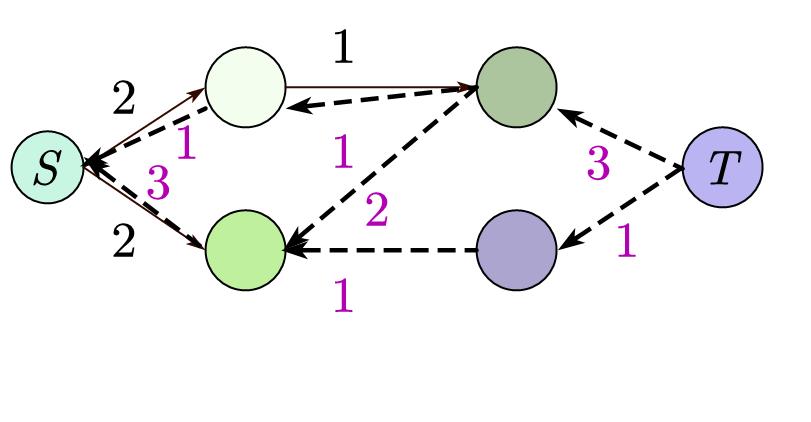
最后我们把刚刚得到的所有 \(w\) 加起来就是最大流。
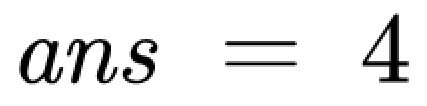
Ford–Fulkerson 算法的时间复杂度为 \(O(fm)\),\(f\) 为最大流大小,\(m\) 为边的数量(可以想一想为什么是 \(O(fm)\))
EK 算法
剩下的部分,终于不用画图了,纯属优化
EK 算法唯一优化的地方是找路径的时候找最短路径,而不是随便找,BFS 就可以实现。
当然,我们是把图当作无权图来对待。

发明者证明了该算法时间复杂度为 \(O(m^2n)\)。
C++代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 210, M = 10010, inf = 0x3f3f3f3f3f3f3f3f;
struct Edge {
int to;
int next;
LL c;
} e[M];
int head[N], idx = 1;
void add(int a, int b, int c) {
idx++;
e[idx].next = head[a];
e[idx].c = c;
e[idx].to = b;
head[a] = idx;
}
int n, m, S, T;
bool vis[N];
int q[N];
int hh, tt;
int pre[N];
LL flow[N];
bool bfs() {
memset(vis, 0, sizeof vis);
vis[S] = 1;
hh = 0, tt = -1;
q[++tt] = S;
flow[S] = inf;
while (hh <= tt) {
int t = q[hh++];
for (int i = head[t]; i; i = e[i].next) {
if (e[i].c) {
int to = e[i].to;
if (vis[to]) continue;
flow[to] = min(flow[t], e[i].c);
vis[to] = 1;
pre[to] = i;
q[++tt] = to;
if (to == T) return 1;
}
}
}
return 0;
}
LL ans;
void update() {
int x = T;
while (x != S) {
int p = pre[x];
e[p].c -= flow[T];
e[p ^ 1].c += flow[T];
x = e[p ^ 1].to;
}
ans += flow[T];
}
int main() {
scanf("%d%d%d%d", &n, &m, &S, &T);
for (int i = 1; i <= m; i++) {
int a, b;
LL c;
scanf("%d%d%lld", &a, &b, &c);
add(a, b, c);
add(b, a, 0);
}
while (bfs()) update();
printf("%lld\n", ans);
return 0;
}
dinic 算法
我们在找最短路径的时候顺便将图分层,从 \(S\) 最少几步可以到达,一个点的层次就是几,但是我们假设到 \(S\) 点本身就需要 \(1\) 步,即 \(S\) 的层次为 \(1\)。
比如:
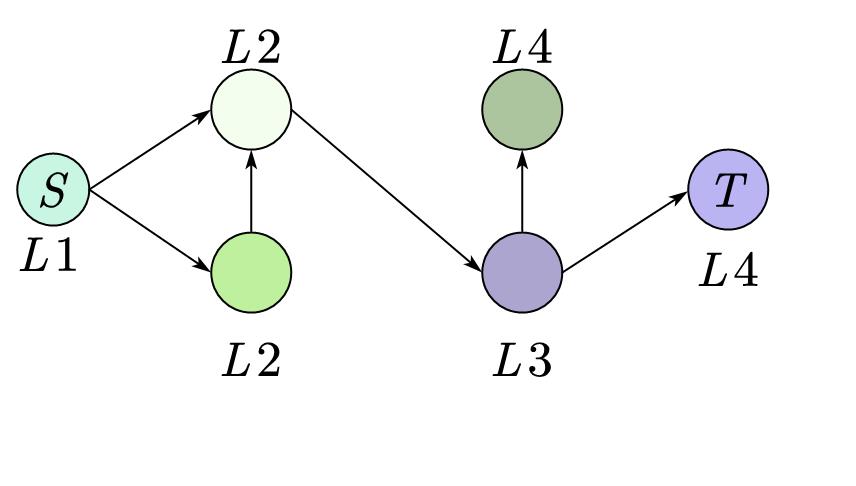
然后我们在找路径的时候,加入我们已经到了 \(u\),下一步我们一定要到下一层的 \(v\),而不是相同层次的点:
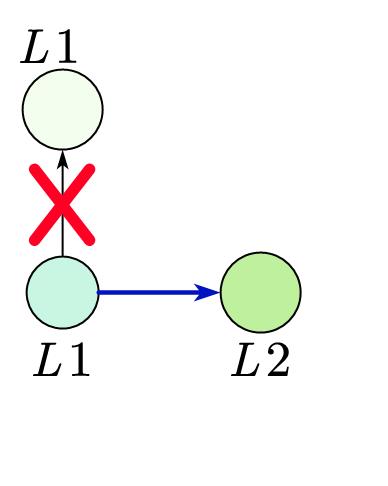
其他内容与 EK 算法相同,算法发明者证明了其时间复杂度为 \(O(n^2m)\)。
C++代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 210, M = 10010, INF = 1e16;
struct edge {
int to, next, w;
} e[M];
int head[N], idx = 1;
void add(int a, int b, int c) {
idx++, e[idx].to = b, e[idx].next = head[a], e[idx].w = c, head[a] = idx;
idx++, e[idx].to = a, e[idx].next = head[b], e[idx].w = 0, head[b] = idx;
}
int n, m, S, T;
int q[N];
int hh, tt;
int d[N];
bool bfs() {
memset(d, 0, sizeof(d));
hh = tt = 0;
q[0] = S;
d[S] = 1;
while (hh <= tt) {
int t = q[hh++];
for (int i = head[t]; i; i = e[i].next) {
int to = e[i].to;
if (!d[to] && e[i].w) {
d[to] = d[t] + 1;
q[++tt] = to;
if (to == T) return true;
}
}
}
return false;
}
int dinic(int u, int limit) {
if (u == T) return limit;
int rest = limit;
for (int i = head[u]; i && rest; i = e[i].next) {
int to = e[i].to;
if (d[to] == d[u] + 1 && e[i].w) {
int k = dinic(to, min(rest, e[i].w));
if (!k) d[to] = 0;
rest -= k;
e[i].w -= k;
e[i ^ 1].w += k;
}
}
return limit - rest;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> S >> T;
for (int i = 1; i <= m; i++) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
int maxflow = 0, flow = 0;
while (bfs()) {
while (flow = dinic(S, INF)) {
maxflow += flow;
}
}
cout << maxflow << '\n';
return 0;
}
费用流
有时,输送水是需要付钱的!
费用流就是在每条管道指定要解决在保证最大流的前提下,付的钱最少。
每条边会有两个权值,\(w, cost\),\(w\) 是边的容量,\(cost\) 是流过单位量的水需要付的钱。
那么怎么解决这个问题呢?
实际上,非常简单,既然要保证最大流,那么还是需要找路径,又要付的钱最少,
那么就相当于每一条边带上了一个权值,我们不能再把它当作无权图来对待了。
您可能已经想到,可以跑最短路,这样既找到路径,又保证费用最小化。
是的,费用流非常简单,只要把网络最大流的 BFS 改成 SPFA 即可,
至于为什么不用 Dijkstra,很显然可能有负边权,但一般遇不到,对这一点有疑惑的可以看看官方抽象的定义。
那我们怎么建反边呢?
容量与最大流一样,就是正边流过了 \(w\),反边就加上 \(w\),
但是价格不太一样,假如正边的价格是 \(cost\),那么反边就是 \(-cost\),因为我们要把钱拿回来。
此时,我们因为用了 SPFA,那么说明费用流的算法就不是基于分层图的,
因为如果像最大流一样 BFS,那么 BFS 到哪一层,哪一层的点一定是最先被访问到的,一定是最短的,
但是加上了权值就不一样了,经过同一层次的点也有可能最短,所以费用流的算法就不是基于分层图的。
我们用 dinic 反而是小题大作,还要分个层,所以我们费用流多用 EK 算法。
C++代码
#include <bits/stdc++.h>
using namespace std;
const int N = 5010, M = 100010, INF = 0x3f3f3f3f;
struct edge {
int to, next, w, cost;
} e[M];
int head[N], idx = 1;
void add(int u, int v, int w, int cost) {
idx++;
e[idx].to = v;
e[idx].next = head[u];
e[idx].w = w;
e[idx].cost = cost;
head[u] = idx;
idx++;
e[idx].to = u;
e[idx].next = head[v];
e[idx].w = 0;
e[idx].cost = -cost;
head[v] = idx;
}
int n, m, S, T;
int dis[N], pre[N], flow[N];
bool st[N];
bool spfa() {
queue<int> q;
q.push(S);
memset(dis, 0x3f, sizeof(dis));
memset(flow, 0, sizeof(flow));
dis[S] = 0;
flow[S] = INF;
st[S] = true;
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = head[t]; i; i = e[i].next) {
int to = e[i].to;
if (e[i].w && dis[to] > dis[t] + e[i].cost) {
dis[to] = dis[t] + e[i].cost;
pre[to] = i;
flow[to] = min(flow[t], e[i].w);
if (!st[to]) {
q.push(to);
st[to] = true;
}
}
}
}
return flow[T] > 0;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> S >> T;
for (int i = 1; i <= m; i++) {
int u, v, w, cost;
cin >> u >> v >> w >> cost;
add(u, v, w, cost);
}
int maxflow = 0, mincost = 0;
while (spfa()) {
maxflow += flow[T];
mincost += flow[T] * dis[T];
int x = T;
while (x != S) {
e[pre[x]].w -= flow[T];
e[pre[x] ^ 1].w += flow[T];
x = e[pre[x] ^ 1].to;
}
}
cout << maxflow << ' ' << mincost << '\n';
return 0;
}